Lecture Board Images
Motivation






Programming in Typed uScheme




Note
On the board, I incorrectly used val or val-rec relative to how they are
defined in the "real" Typed μScheme. A val-rec needs to be given a type
annotation and can only be used with a lambda-expression. The type annotation
is necessary for type checking (because we must record the name in the typing
environment with its type in order to check recursive uses). The restriction to
lambda-expressions is simple, but it could be relaxed to zero or more
type-lambda expressions around a lambda-expression. The examples would be
better written as:
(val-rec [ length : (forall ('a) ((list 'a) -> int)) ]
(type-lambda ('a)
(lambda ([ xs : (list 'a) ])
(if ((@ null? 'a) xs)
0
(+ 1 ((@ length 'a) ((@ cdr 'a) xs)))))))
(val-rec [ map : (forall ('a 'b) (('a -> 'b) (list 'a) -> (list 'b))) ]
(type-lambda ('a 'b)
(lambda ([ f : ('a -> 'b) ] [ xs : (list 'a) ])
(if ((@ null? 'a) xs)
(@ '() 'b)
((@ cons 'b) (f ((@ car 'a) xs)) ((@ map 'a 'b) f ((@ cdr 'a) xs)))))))
(val o ; compose
(type-lambda ('a 'b 'c)
(lambda ([ f : ('b -> 'c) ] [ g : ('a -> 'b) ])
(lambda ([ x : 'a]) (f (g x))))))Typed uScheme Typing Judgements and Rules




Motivate capture avoiding substitution
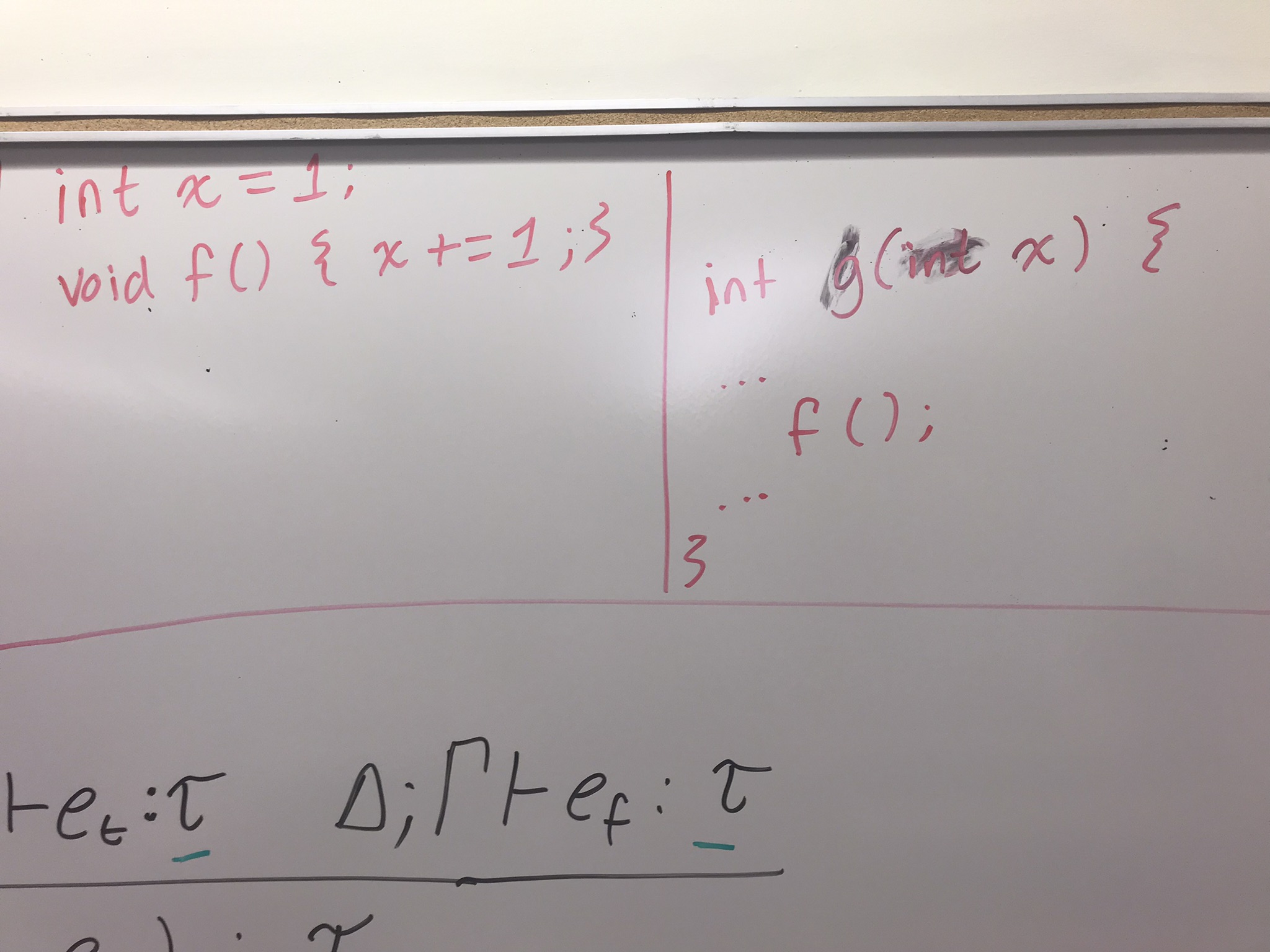
Kinds

